Pipeline Bend Computer Simulation

The induction bending process for large-diameter pipes is very popular technology. An important problem in the bending process is prediction and improvement of the bending quality. In this article, a thermo-elastic-plastic mechanical model is used to simulate induction bending of large-diameter pipes. The bending experiments of the API 5L X65 induction bend pipes were performed to clarify the deformation behavior of the pipes. The large deformation behaviors of these experiments were simulated by finite element method, using ADINA software.

Triple D Bending has been bending pipe for 26 years and induction bending for seven years. Customer specifications and requirements for material properties are becoming increasingly stringent and the company is continually improving processes to meet these requirements. For some customer applications, ovality of the pipe bends is of major concern. For this reason Triple D Bending desired to have a method of predicting the ovality of completed bends in order to find ways to improve the ovality of the pipe bends.

In pipe production, pipe bending using local induction heating is an advanced technique to produce large diameter pipes with a large or small bend radius.

Induction bending as a technique is relatively quick and cheap, but induction bending can produce unwanted changes in geometry such as wall thinning at the extrados, wall thickening and wrinkling at the intrados, and steep transitions in wall thickness between tangent and bend. These problems increase in severity as the bend radius is reduced. However, there are a lot of other problems, such as springback and cross-section ovality when bending thinwall pipe with a large diameter.

• Pipe diameter ØD = 30-inches (762 mm),
• Wall thickness t = 0.562 inch (14.27 mm),
• Material     API 5L X65,
• Bend radius     R = 189 inches (4800 mm),
• Bend angle     φ= 90°.

The fundamental tasks which had to be solved can be summarized as follows:

• material characteristics identification;
• implementation of material characteristics into computational model;
• finite element modelling (geometry, definition of thermal contact problem, thermo-plasticity and large strain analysis);
• FE stress, strain, displacement analysis;
• computational ovality prediction.

Line pipe for constructing oil and gas pipelines is made from steel, and in particular, either low-carbon steel or low-alloy steel. Low-carbon or low-alloy steels are suitable for line pipe materials and most other steel structures such as buildings or bridges because they provide a durable, strong material to withstand the service loads imposed on such structures. Other iron-based materials such as wrought iron and cast iron are either too low strength or too brittle to function well as structural materials.

Stainless or high-alloy steels are essential for special applications such as in high-temperature piping and pressure vessels or tool steels, but they are not suitable and cannot be made economically in the quantities needed for use in structures including pipelines. Only low-carbon steels or low-alloy steels offer the appropriate ranges of desirable properties (i.e., strength, toughness, ductility and weldability) that are required for structural applications.

The performance of steels depends on the properties associated with their microstructures. Each type of microstructure and product is developed to characteristic property ranges by specific processing routes that control and exploit microstructural changes. Carbon steels and low-alloy steels with ferrite-pearlite or ferrite-bainite microstructures are used extensively at elevated temperatures. Carbon steels are often used up to about 370ºC under continuous loading, but also have allowable stresses defined up to 540ºC. Effect of elevated-temperature exposure on the room-temperature tensile properties of normalized 0.17% C steel after exposure (without stress) to indicated temperature for 83,000 hours is shown in Figure 1.

The allowable design stresses for steels at elevated temperatures may be controlled by different mechanical properties, depending on the application and temperature exposure.

In designing components that are to be produced from low-alloy steels and to be exposed to temperatures up to 370ºC, the yield and ultimate strengths at the maximum service temperature can be used much as they would be used in the design of components for service at room temperature.

During operation, microstructure of experimental steel XH API 5L X65 is exposed to different levels of temperatures, thus we need to account for the influence of temperature on the behavior of this structural steel. Mechanical properties of a structural steel vary with temperature. In material behavior, changes in temperature can cause the following effects: 1) elastic constants (e.g., E, ν) of the material can change; 2) strain can develop without mechanical loading; 3) material yield strength decreases with increase in temperature; and 4) the material can lose ductility with decrease in temperature.

For the material properties, analysis at room and elevated temperatures were selected as the experimental methods – mechanical properties tests (tensile test) and mathematical approximation of statistical data. The results, tensile test at room temperature and other mechanical characteristics are presented in Table 1.

Table 1: Mechanical properties of API 5L X65 at room and elevated (850ºC) temperature.

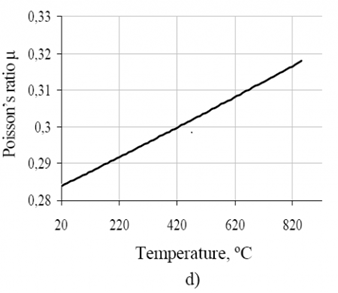
For many structural materials, a change in temperature of a few tens of degrees Celsius from room temperature may not result in much change in the elastic constants. At high enough temperatures, the stiffness and strength of structural steels may be reduced even if the ductility increases. Elevated temperature values of elastic modulus can be determined during tensile testing or dynamic testing. Figure 2 a) shows values of elastic modulus API 5L X65 between room temperature and elevated temperature. The influence of elevated temperature on Yield strength, Ultimate tensile strength and Poisson’s ratio are shown in Figure 2 a) to Figure 2 d). These results were determined during static tensile loading and the statistical data obtained using mathematical approximation.

Figure 2 a), b), c), d): Effect of elevated temperature on mechanical characteristic API 5L X65.

Final values of mechanical parameters at the temperature of 850ºC were obtained from extrapolated curve lines shown in Figure 3, where: σ is engineering stress, ε is engineering strain, E is modulus of elasticity or Young’s modulus at room temperature, E850ºC is modulus of elasticity or Young’s modulus at elevated temperature, H is isotropic hardening modulus at room temperature, and H850ºC is isotropic hardening modulus at elevated temperature. These values were used as input parameters for the FEM analysis of bending process.

Figure 3: Schematic view of temperature dependent material bilinear model.

Computational Assumptions
The finite element method was used for modeling the process of induction bending (Figure 4). The computational model contains the following assumptions:

• The model is built as a half model satisfying symmetrical, boundary and initial conditions.
• They are considered large displacements and large strains (enable to model the shape changes and plasticity during calculation).
• A temperature dependent material bilinear model is needed (Figure 3).
• Induction heating is substitute by heat transfer in contact between bodies (in inductor position, bodies which come into contact by pipe have temperature equal 850˚C, occur heating of pipe material). Contact is modeled without friction and contact pressure is considered 1 MPa.
• Water cooling system is substitute by heat transfer in contact between bodies (in water cooling system position, bodies which come into contact by pipe have temperature equal 20˚C, occur cooling of pipe material). Contact is modeled without friction and contact pressure is 1 MPa.
• Guiding devices are substitute by tight contact surface which come into contact with pipe during simulation, contact is modelled without friction.
• The movement of the pipe is imposed in the free end by velocity equal 0.0018 m s-1.
• The solution time is 18,720 seconds and corresponds to bending of pipe about 90˚.
• Pipe diameter is 762 mm, wall thickness is 14.27 mm and bending radius is 4,800 mm.

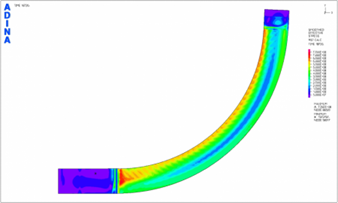
Figure 4: Finite element model of induction bending process.

Necessary inputs for modeling of technological process of the induction bending of pipes:

• accurate geometrical characteristics of device (inductor position, water cooling system position, pipe diameter, wall thickness, bending radius, guiding device position, displacement velocity, initial temperature of pipe);
• material characteristics (Young’s modulus, Poisson’s ratio, Yield strength, isotropic hardening modulus, coefficient of thermal expansion) for temperature range 20 - 850˚C.

Finite Element Modeling Process
The modeling process is realized by using the “classic” finite element computational approach. The Grab mechanism is substituted by a set of solid elements inside the pipe. The bending arm is modeled as two rigid truss elements (Figure 4). These trusses are connected to pin (center of the bending) and solid elements substitute for the grab mechanism. There is in the pin no degree of freedom. In this manner, the bending arm, grab mechanism and pipe may freely rotate around the pin. The grab mechanism is modelled as one layer of solid elements inside the pipe. Low number of elements is used to simulate the bending arm and the grab mechanism, reducing bandwidth of the stiffness matrix [2,6].

The induction bending process is characterized by energy lost from the material surface to the environment. Conduction, convection and radiation cause non-constant temperature distribution across the pipe wall. In order to determine the temperature difference between the outer and inner wall surfaces a thermal FE analysis was performed. There are two thermal boundary conditions applied. First is boundary convection, second is boundary radiation. These boundary conditions are applied on the inner and outer face of the pipe. Application of these boundary conditions and heating mechanism causes the temperature gradient from the outer to the inner face of the pipe. These differences of surface temperatures are low and therefore it can be neglected.

The chosen results of the computational simulation are presented in Figure 5 and Figure 6. Ovalization of the pipe cross-section shall be limited in design to prevent section collapse. The pipe diameter changes are evaluated in two directions: first is in the radial direction, second is in the binormal direction. These changes of diameters are dependent on the angle of the bending arm (Figure 7). The pipe was 30-inch/762 mm - API 5L X65. The applied bending angle was taken from range 0 to 90 degrees. Bend radius was 4800 mm and wall thickness was 0.562 inch / 14.27 mm.

Figure 5. Distribution of plastic strains (plastic deformation).

Figure 6: Von Mises stress distribution after bending process.

Figure 7. Ovality behavior measured during induction bending test realized by computational finite element analysis.

Conclusion
This article presents finite element analysis of the complicated technological problem. The results of the analysis provide information about shape (diameter) changes of the bending pipe. The computational process complicates temperature dependence of the material characteristics and the substitution of induction heating.

Induction heating is a physically complex action. Modeling of this process is not included in FEM software for such structural problems. For this reason it is necessary to substitute induction heating by contact between bodies with heat transfer. Using this substitution simplifies the whole FE model; on the other hand, this solution has the right accuracy.

The main goal of this material has been to present the possibilities of the finite element analysis in the induction bending process of large-diameter pipes. The results of the introduced simulation approach can be summarized as follows: 1) analysis of the residual stress, strain and displacement distribution in pipe; 2) analysis of the plastic stress, strain and displacement distribution in pipe; 3) analysis of the temperature distribution; and 4) analysis of the pipe shape modification – ovality modification.

 

References: “Computer Simulation of Induction Bending Process”. http://pipelineandgasjournal.com/computer-simulation-induction-bending-process. January 2014.